Chapter 5 Exercises
-
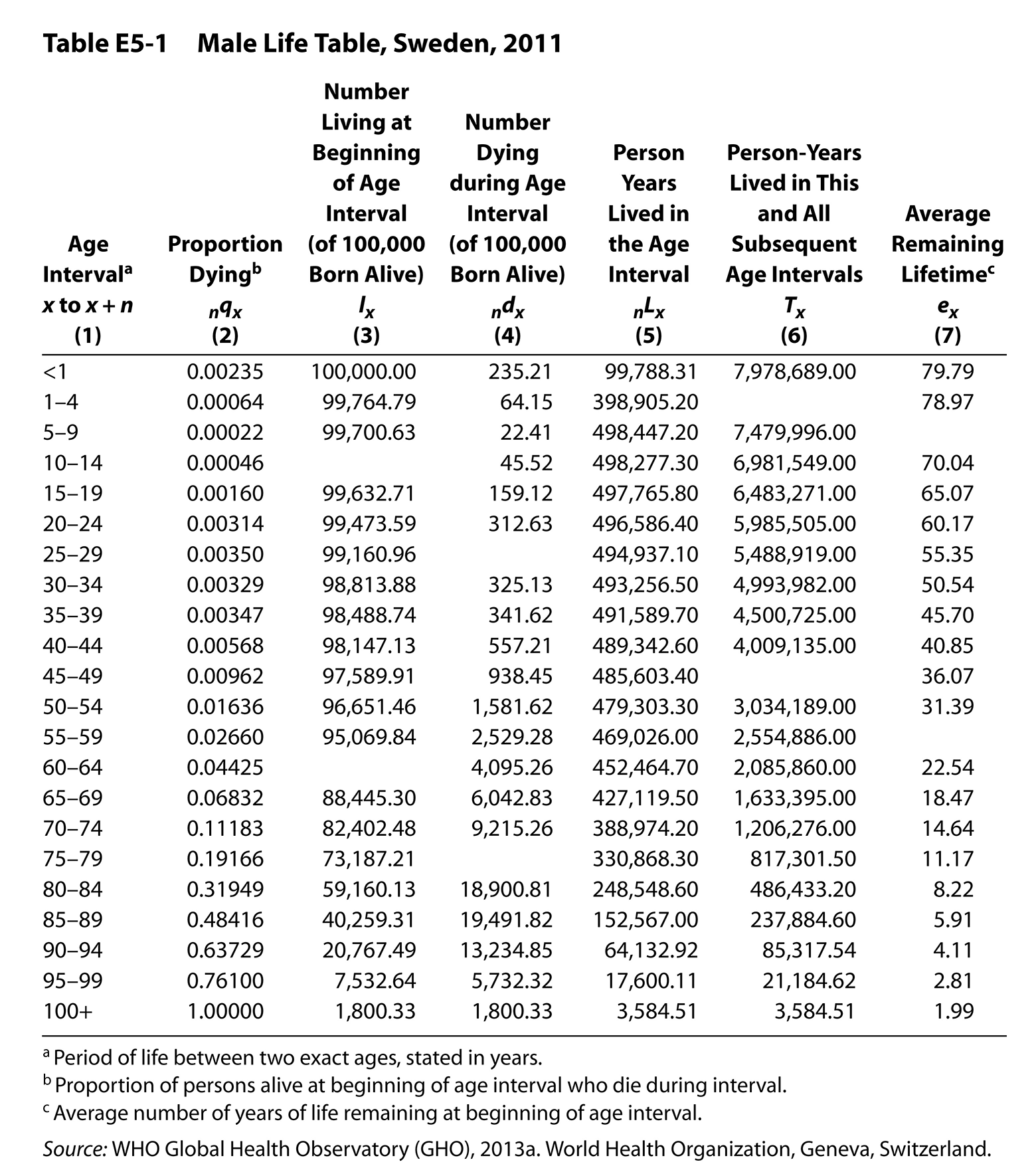
Table E5-1 on p. 181 is a male life table for Sweden according to the age-sex-specific death rates of 2011. Some blanks intentionally have been left in columns 3, 4, 6, and 7 of the table. Your task is to fill in those blanks, copying the computations used for determining the other entries for the same columns. What follows is an explanation of each of the columns, from left to right:
-
Column 1 simply lists the age intervals. With two exceptions, we have used five- year intervals rather than single-year ones; thus, this is an “abridged” life table. The exceptions are at either end of the age range. Infant mortality (age zero to one) is separated from early childhood mortality (age one to four). The terminal category (100 and over in this table) is open-ended.
-
Column 2 (nqx) presents the assumed risk of dying over the n years beginning at age x for each of the age intervals. Each such “mortality rate” is based on an age- sex-specific death rate. The entire rest of the table is generated from column 2.
-
Column 3 (lx) and column 4 (ndx) are best explained together. We start at the top of column 3 with an arbitrary, large, hypothetical cohort (or “radix”); this table follows the convention of using 100,000. Then we trace what the fate of this hypothetical cohort would be if it experienced the probabilities of death listed in column 2. For instance, the 100,000 men born experienced a probability of death of 0.00235 until their first birthday. This would result in 235.21 deaths by the first birthday. This is the entry for column 4 for the first age interval. How many men would start their second year of life? We subtract the deaths (235.21) from those who started the first interval (100,000) and get 99,764.79, the next entry in column 3. Multiplying these 99,764.79 survivors by the probability of dying between the ages of one and four, or 0.00064, we find that 64.15 of them will die, the next entry in column 4, and so on, back and forth between columns 3 and 4. Algebraically stated,
ndx = (nqx)(lx)
and
lx+n = lx – nd
where
x = exact age at the beginning of the age interval n = number of years in the age interval -
Column 5 (nLx) is the number of person-years lived in the age interval by the survivors of the hypothetical cohort. In the first row, if there were 100,000 babies born and 99,788 survived the whole first year, how many person-years did they collectively live during that one-year age interval? It depends on when during the year death occurred. Because of the unusual pattern of death during infancy, demographers use a complex procedure to arrive at an estimate for the top entry in column 5. For subsequent age intervals, however, deaths are more evenly spread throughout the interval. Thus, for most of the age intervals beyond infancy, the entry will be very close to the average of (1) the number of people alive at the beginning of the interval and (2) the number alive at the end of the interval. You are not required to make such a complex interpolation here.
-
Column 6 (Tx) is derived entirely from column 5 (nLx). It tells how many person-years will be lived by the survivors of the hypothetical cohort from any specified age until all are dead. Thus, the entry 7,978,689 at the top of column 6 indicates this hypothetical cohort collectively will have that many years of life among them before the last one dies. Arithmetically, the column is constructed by summing the number of years lived in each interval from the bottom row upward to the top in column 5. Stated algebraically,
-
Column 7 (ex) tells the life expectancy remaining after each specified birthday. Take the top entry as an illustration, the life expectancy at birth (e0). If there were 7,978,689 person-years of life to be shared among the 100,000 males who were born
-
Consult Table E5-1 to arrive at the following figures:
-
From the nqx column, find the percentage of the cohort reaching their sixty-fifth birthday that would survive to their seventieth birthday:
-
From the lx column, find the number of the cohort who would reach their sixty-fifth birthday:
-
What number of cohort members die between their sixty-fifth and seventieth birthdays:
-
What is the number of person-years lived by the cohort between ages sixty-five and seventy:
-
What is the average remaining years of life at age sixty-five and what is the total life expectancy a sixty-five-year-old can expect:
-
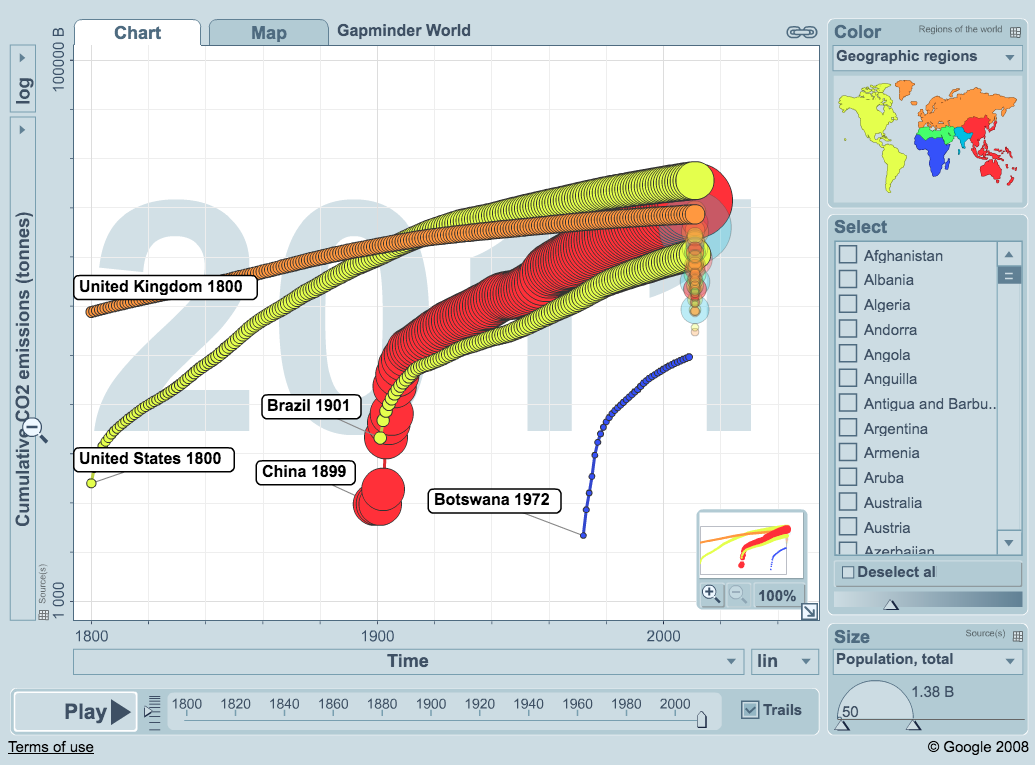
Click on the graph. We are focusing on four countries: Bangladesh, China, Niger, and United Kingdom from 1840 through 2012. Hit play at the bottom left. After the interactive chart plays itself out answer the following questions:
-
Write down the year and associated fertility rate and child mortality rate for each country at the beginning of the period and at the end of the period shown on the chart. What is their relationship with each other?
*Beginning years shown here are the years in which both fertility rate and child mortality rate become available. *2013 data became available after the publication of this textbook.
-
Why do you think the time periods all have different starting points?
-
What is the relationship between fertility and child mortality rates?
-
Which of the countries experienced the largest total decline in child mortality from beginning until end of the periods graphed?
Now click on the y-axis and change the measure from fertility to income per person. Click play. How do the trend lines change when using income instead of fertility? Why?
Charts

Figure 5.1
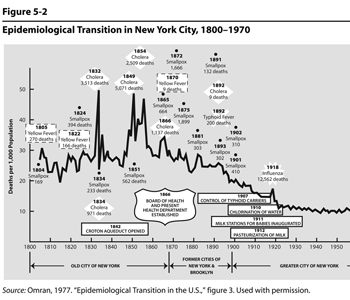
Figure 5.2
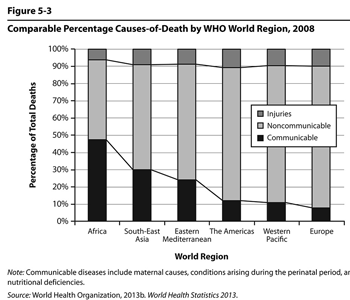
Figure 5.3
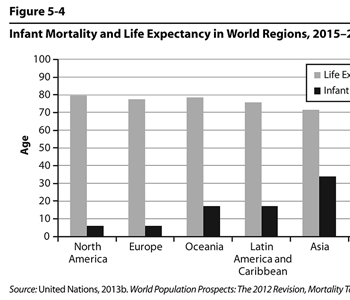
Figure 5.4
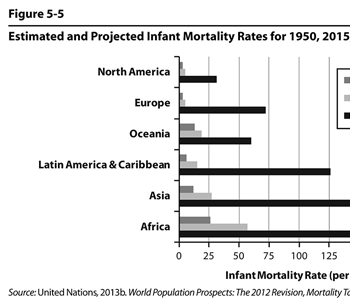
Figure 5.5
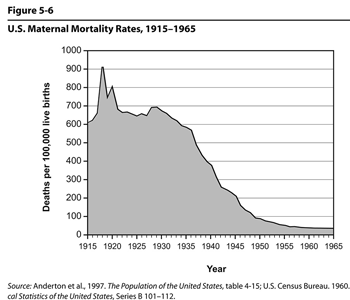
Figure 5.6
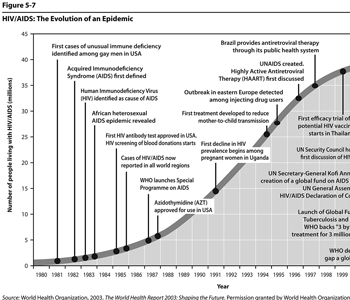
Figure 5.7
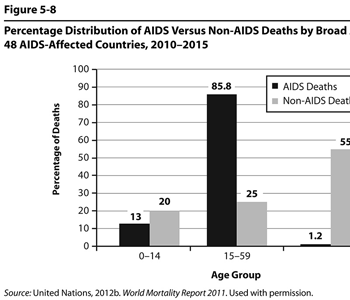
Figure 5.8
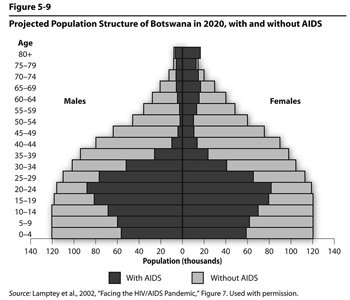
Figure 5.9